Zusammenfassung
Lernen Sie die mathematischen Funktionen von VBA kennen.
Techniken
VBA, mathematische Funktionen
Voraussetzungen
Access 97 und höher
Roland Grothe, Hanau, und André Minhorst, Duisburg
„Mathe! – Gut, dass ich damit seit der Schulzeit (seit dem Studium) nichts mehr zu tun habe!“ – das denken jetzt möglicherweise einige Leser. Früher oder später holt einen diese Zeit wieder ein, denn auch wenn die trigonometrischen Funktionen von VBA eher selten zum Einsatz kommen dürften, gibt es durchaus interessante Kandidaten: Oder behauptet da irgendjemand, er habe noch nie beispielsweise eine Zufallszahl ermitteln müssen
In diesem Beitrag stellen wir Ihnen die mathematischen Funktionen von VBA vor. Wenn auch die meisten dieser Funktionen nur in recht speziellen Anwendungen zum Einsatz kommen werden, sind doch einige darunter, die Ihnen auch bei der Lösung ganz „normaler“ Entwicklerprobleme hilfreich zur Seite stehen.
Mathematische Funktionen sind prinzipiell nichts anderes als eine für den Anwender vereinfachte Form der Eingabe komplizierter Berechnungen.
Durch die Verwendung der eingebauten mathematischen Funktionen werden Ihre Anwendungen übersichtlicher und Ihre Gedankengänge bei der Entwicklung auch für andere Benutzer nachvollziehbar. Tab. 1 zeigt in einer übersicht die in diesem Beitrag besprochenen Funktionen.
Anzumerken ist dabei, dass die englischen Funktionen in VBA und SQL und die deutschen Varianten beispielsweise im Abfrageentwurf, im Ausdruckseditor oder in Eigenschaften von Datenbankobjekten oder Steuerelementen zum Zuge kommen.
Um Ihnen das Ausprobieren der hier beschriebenen Funktionen zu erleichtern, enthält die Beispieldatenbank das Formular frmBeispielmathematischeFunktionen, in dem Sie eigene Parameter zuweisen und sich die jeweiligen Resultate aller Funktionen ansehen können. überschreiben Sie dazu einfach die vorgegebenen Werte in den Eingabefeldern.
Diese oft auch als trigonometrische oder Kreisfunktionen bezeichneten Funktionen stellen in der elementaren Geometrie die Seitenverhältnisse in einem rechtwinkligen Dreieck dar.
Alle Funktionen erwarten als Parameter einen Zahlenwert, der entweder einen Winkel im Bogenmaß (Sin(), Cos(), Tan()) oder das Verhältnis zweier Seiten des Dreiecks (Atn()) angibt.
|
Funktion (englische Bezeichnung) |
Funktion (deutsche Bezeichnung) |
Ergebnis/Beschreibung |
|
Sin(Zahl) |
Sin(Zahl) |
Sinus des Winkels Zahl (im Bogenmaß) |
|
Cos(Zahl) |
Cos(Zahl) |
Kosinus des Winkels Zahl (im Bogenmaß) |
|
Tan(Zahl) |
Tan(Zahl) |
Tangens des Winkels Zahl (im Bogenmaß) |
|
Atn(Zahl) |
ArcTan(Zahl) |
ArkusTangens des Winkels Zahl (Ergebnis im Bogenmaß) |
|
Abs(Zahl) |
Abs(Zahl) |
Absolutwert des Arguments Zahl |
|
Exp(Zahl) |
Exponential(Zahl) |
Exponentialwert des Arguments Zahl |
|
Log(Zahl) |
Logarithmus(Zahl) |
Natürlicher Logarithmus des Arguments Zahl |
|
Int(Zahl) |
Int(Zahl) |
Nächstkleinere Ganzzahl des Arguments Zahl |
|
Fix(Zahl) |
Fix(Zahl) |
Ganzzahliger Anteil des Arguments Zahl |
|
Rnd(Zahl) |
ZZG(Zahl) |
Zufallszahl. Das optionale Argument Zahl bestimmt, wie die Zufallszahl ermittelt wird. |
|
Sgn(Zahl) |
Vorzchn(Zahl) |
Vorzeichen des Arguments Zahl |
|
Sqr(Zahl) |
QWurzel(Zahl) |
Quadratwurzel des Arguments Zahl |
Tab. 1: Mathematische Funktionen und ihre Beschreibung
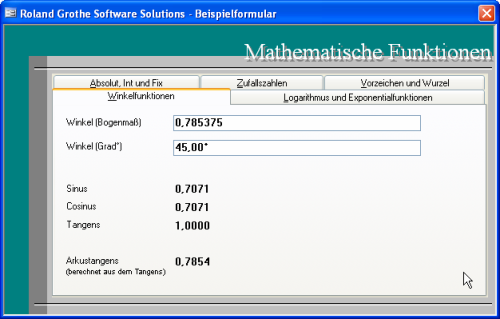
Bild 1: In der Beispieldatenbank sehen Sie die Ergebnisse aller in diesem Kapitel behandelten Funktionen.
Die Funktion Sin()
Die Funktion berechnet aus einem Winkel das Längenverhältnis der dem Winkel gegenüberliegenden Seite (Gegenkathete) zu der Hypothenuse (längste Seite) eines rechtwinkligen Dreiecks. Als Parameter muss der Winkel im Bogenmaß angegeben werden. Steht eine Winkelangabe nur in Grad zur Verfügung, muss diese zuvor in das Bogenmaß umgerechnet werden. Die Formel dazu lautet folgendermaßen:
Bogenmaß = Grad * Pi / 180
Dabei ist Pi eine mathematische Konstante mit dem Näherungswert 3,1415926535897932. Statt diese Konstante direkt im Code anzugeben, kann man sie auch mit folgender Funktion berechnen lassen:
Pi = 4 * Atn(1)
Um in einem berechneten Steuerelement (siehe Bild 1) beispielsweise den Sinus eines Winkels, dessen Größe in einem Formularfeld txtWinkelB definiert ist, zu berechnen, verwenden Sie folgende Syntax für die Eigenschaft Steuerelementinhalt:
=Sin([txtWinkelB])
Statt eines direkten Feldbezugs kann auch ein komplexerer Ausdruck an die Funktion übergeben werden.
Dies ist zum Beispiel dann notwendig, wenn die Winkelangabe nur in Grad verfügbar ist, wie in folgendem Beispiel:
= Sin([txtWinkelG] * 3,1415926535897932/180)
Das Ergebnis ist ein Wert des Datentyps Double im Bereich von -1 bis 1.
Die Funktion Cos()
Der Cosinus ist die Gegenfunktion des Sinus und liefert das Längenverhältnis der dem Winkel anliegenden Seite (Ankathete) zu der Hypothenuse eines rechtwinkligen Dreiecks.
Auch hier ist als Parameter der Winkel im Bogenmaß anzugeben:
=Cos([txtWinkelB])
Das Ergebnis ist ein Wert des Datentyps Double im Bereich von -1 bis 1.
Die Funktion Tan()
Der Tangens liefert das Längenverhältnis der dem Winkel gegenüberliegenden Seite (Gegenkathete) zu der dem Winkel anliegenden Seite (Ankathete) eines rechtwinkligen Dreiecks.
Auch hier muss als Parameter der Winkel im Bogenmaß angegeben werden:
=Tan([txtWinkelB])
Das Ergebnis ist ein Wert des Datentyps Double, wobei der Wert im Bereich der Winkel 90° und 270° extrem groß wird.
Die Funktion ArcTan()
Der Arkustangens ist die Umkehrfunktion der Funktion Tan() und berechnet aus dem Längenverhältnis der dem Winkel gegenüberliegenden Seite (Gegenkathete) zu der dem Winkel anliegenden Seite (Ankathete) eines rechtwinkligen Dreiecks dessen Winkel im Bogenmaß:
=Atn([txtWinkelB])
Das Ergebnis ist ein Wert des Datentyps Double zwischen -Pi/2 und Pi/2.
Ende des frei verfügbaren Teil. Wenn Du mehr lesen möchtest, hole Dir ...
den kompletten Artikel im PDF-Format mit Beispieldatenbank
diesen und alle anderen Artikel mit dem Jahresabo
